Question

A news article estimated that only 5% of those age 65 and older who prefer to watch the news, rather than to read or listen, watch the news online. This estimate was based on a survey of a large sample of adult Americans. Consider the population consisting of all adult Americans age 65 and older who prefer to watch the news, and suppose that for this population the actual proportion who prefer to watch online is 0.05.

A random sample of n = 100 people will be selected from this population and p, the proportion of people who prefer to watch online, will be calculated. what are the mean and standard deviation of the sampling distribution of p? (Round your standard deviation to four decimal places.)
mean_________________
standard deviation _______________

Answer 1

Mean = 0.05

Standard deviation = 0.02179

Explanation:

Data provided in the question:

People of age 65 and older who prefer to watch the news rather than to read or listen, watch the news online, p = 5% = 0.05

Sample size, n = 100

Now,

q = 1 - p

⇒ q = 1 - 0.05 = 0.95

If the random samples are selected from the population with the population proportion of 'p' then the mean is given as

Mean = p

or

Mean = 0.05

And,

Standard deviation =
`\sqrt{(pq)/(n)}`

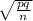
or

Standard deviation =
`\sqrt{(0.05*0.95)/(100)}`

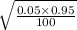
or

Standard deviation = 0.02179