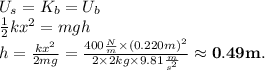Question

A 2.00-kg block is pushed against a spring with negligible mass and force constant k = 400 N/m. compressing it 0.220 m. When the block is released, it moves along a frictionless, horizontal surface and then up a frictionless incline with slope 37.0 degree. What is the speed of the block as it slides along the horizontal surface after having left the spring? How far does the block travel op the incline before starting to slide back down?

Answer 1

The block's speed as it slides horizontally is 3.11 m/s, approximately. As going up on the ramp, it reaches a 0.49 m height before turning back.

Step-by-step explanation:

As the spring is compressed, it stores elastic potential energy

`U_s = (1)/(2) kx^2`,

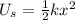as soon as it's released, assuming no loss in the transfer, all the energy is transfered to the block, which adquires kinetic energy

`U_s = K_b \\ (1)/(2) kx^2 = (1)/(2) m v_b^2`.

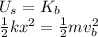From this last one, we can write for the block's velocity

`v_b = \sqrt{(kx^2)/(m)} = \sqrt{(400(N)/(m)* \left(0.220 m\right)^2)/(2kg)} \approx \mathbf{3.11 m\s}.`

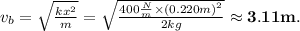
Last, when the block reaches the ramp, as it goes up, all its kinetic energy becomes gravitational potential energy, i.e.,

`U_s = K_b = U_b \\ (1)/(2)kx^2 = mgh \\ h = (kx^2)/(2mg) = (400(N)/(m)*\left(0.220 m\right)^2)/(2* 2 kg* 9.81 (m)/(s^2)) \approx \mathbf{0.49 m}.`