Answer:
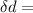 +/- 0.01 mm
+/- 0.01 mm
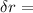 +/- 0.02 mm
+/- 0.02 mm
Explanation:
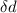 . The error of a quantity directly measured is the uncertainty of the tool used for measuring. So error for diameter is 0.01 mm.
. The error of a quantity directly measured is the uncertainty of the tool used for measuring. So error for diameter is 0.01 mm.
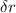 . The error of a quantity obtained multiplying/dividing a measure by a constant is calculated multiplying/dividing the measure uncertainity by the same constant. Radius is calculated as r=2*d, so we calculate
. The error of a quantity obtained multiplying/dividing a measure by a constant is calculated multiplying/dividing the measure uncertainity by the same constant. Radius is calculated as r=2*d, so we calculate
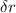 multiplying the diameter uncertainty by 2 (
multiplying the diameter uncertainty by 2 (
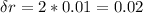 ).
).