Question

Someone help me with this

Answer 1

A) t = 1 second to reach the highest point

B) h = 96 feet

C) t = 3.449 seconds to hit the ground

Explanation:

We notice that the equation that describes the position of the object in terms of the time, is a parabola (quadratic) with negative leading coefficient. therefore this is a parabola with arms pointing down, and with vertex at the top. It is at that top vertex that the maximum altitude of the object is reached.

We need therefore to find the position of the vertex (time "t" is the horizontal coordinate and height "h" is the vertical coordinate).

We know that the vertex (maximum of a parabola of this type - normally described by
`y=ax^2+bx+c`) is given by
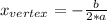`x_(vertex) = -(b)/(2*a)`. Therefore in our case, understanding that time "t" is equivalent to the variable "x", and eight "h" is equivalent to the variable "y", that "-16" is
`a`, and "32" is
`b`, we have that the maximum occurs for:

`t_(max)=-(32)/(2*(-16)) = (-32)/(-32) = 1`

which means at one second from the launching.

We then can find the answer to part B by replacing t with "1" second in the formula for the height "h":

`h(1)=-16*(1)^2+32(1)+80=-16+32+80=96`

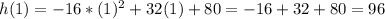
That is : a height of 96 feet.

To find the answer for part C: the time to hit the ground, we solve for the variable "t" in the given expression for the height, by setting the height to zero (object touching the ground) and using the quadratic formula:

`0=-16t^2+32t+80\\t=(-32+/-√(32^2-4*(-16)*80) )/(2*(-16)) \\ t=(-32+/-√(6144) )/(-32)`

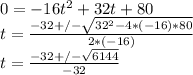
which gives us two solutions: t = -1.449 seconds, and t = 3.449 seconds

Since the negative time does not have physical meaning in our case (time before the object was launched), we adopt the second answer: t = 3.449 seconds