For this case we propose a system of equations:
x: Let the variable representing the age of the first child of the Smiths
y: Let the variable representing the age of the second child of the Smiths
According to the data of the statement we have to:
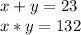
From the first equation we have to:
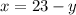
We substitute in the second equation:
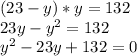
We find the solutions by factoring:
We look for two numbers that, when multiplied, result in 132 and when added, result in 23. These numbers are 11 and 12.
Thus, we have that the factorized equation is:
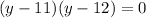
Thus, the solutions are:
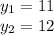
So, we can take any of the solutions:
With
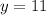
Then

Therefore, the ages of the children are 11 and 12 respectively.
Answer:
The ages of the children are 11 and 12 respectively.