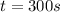Answer: 300 s
Step-by-step explanation:
The momentum
 is given by the following equation:
is given by the following equation:
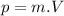
Where
 is the mass of the object and
is the mass of the object and
 is the velocity.
is the velocity.
In addition, according to the conservation of linear momentum, we have:
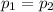 (1)
(1)
Where:
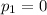 is the initial momentum of the astronaut, which is initially at rest
is the initial momentum of the astronaut, which is initially at rest
 is the final momentum, being
is the final momentum, being
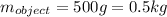 ,
,
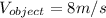 and
and
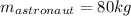
Then (1) is rewritten as:
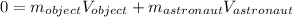 (2)
(2)
Finding te velocity of the astronaut
 :
:
 (3)
(3)
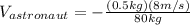 (4)
(4)
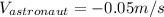 (5) The negative sign of the velocity indicates it is directed towards the spaceship, however its speed (the magnitude of the velocity vector) is positive
(5) The negative sign of the velocity indicates it is directed towards the spaceship, however its speed (the magnitude of the velocity vector) is positive

On the other hand we have the following:
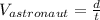 (6)
(6)
Where
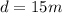 the distance between the astronaut and the spacheship and
the distance between the astronaut and the spacheship and
 the time. So, we have to find
the time. So, we have to find
 :
:
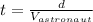 (7)
(7)
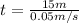
Finally: