Question

Based on the data collected, explain why a launch angle of 30 degrees (HIGH HORIZONTAL VELOCITY & SMALL TIME OF FLIGHT) will allow a projectile to go just as far when the launch angle of 60 degrees (LOW HORIZONTAL VELOCITY AND LARGE TIME OF FLIGHT).

Answer 1

Step-by-step explanation:

The horizontal distance traveled by the projectile is given by the formula

`R=(u^(2)Sin2\theta )/(g)`

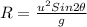
The formula for the time of flight is given by

`T = (2u Sin\theta )/(g)`

Case I: when the launch angle is 30°

So,
`R_(1)=(u^(2)Sin60 )/(g)`

`R_(1)=(0.866u^(2))/(g)`

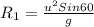
Horizontal velocity = u Cos 30 = 0.866 u

`T_(1) = (2u Sin30 )/(g)=(u)/(g)`

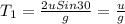
Case II: when the launch angle is 60°

`R_(2)=(u^(2)Sin120)/(g)`

`R_(2)=(0.866u^(2))/(g)`

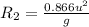
Horizontal velocity = u Cos 60 = 0.5 u

`T_(1) = (2u Sin60 )/(g)=(1.73 u)/(g)`

By observing the case I and case II, we conclude that

R1 = R2

Horizontal velocity 1 > Horizontal velocity 2

T1 < T2