Answer:
The bonus will be paid on at least 4099 units.
Explanation:
Problems of normally distributed samples can be solved using the z-score formula.
In a set with mean
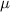 and standard deviation
and standard deviation
 , the zscore of a measure X is given by
, the zscore of a measure X is given by
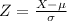
After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the percentile of this measure.
In this problem, we have that:
The highest 5 percent is the 95th percentile.
Past records indicate that, on the average, 4,000 units of a small assembly are produced during a week. The distribution of the weekly production is approximately normally distributed with a standard deviation of 60 units. This means that
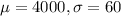 .
.
If the bonus is paid on the upper 5 percent of production, the bonus will be paid on how many units or more?
The least units that the bonus will be paid is X when Z has a pvalue of 0.95.
Z has a pvalue of 0.95 between 1.64 and 1.65. So we use
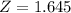
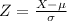
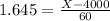
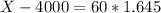
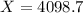
The number of units is discrete, this means that the bonus will be paid on at least 4099 units.