Question

A study of driving costs based on 2012 medium-sized sedans found that the average cost (car payments, gas, insurance, upkeep, and depreciation) in cents per mile is approximately:

C(x) = 1910.5/x^1.72 + 42.9 (5 ≤ x ≤ 20)

Where x (in thousands) denotes the number of miles the car is driven each year.

Show that the graph of C is concave upward on the interval (5, 20).

Answer 1

Since the second derivative is positive for any value of the given interval then we can conclude that the graph of C is concave upwards on the interval (5, 20).

Explanation:

We can find the second derivative of the function C(x) in order to determine its concavity.

To make the derivative process easier, we can begin rewriting it using negative exponents but no fractions using exponent properties.

`C(x) = 1910.5 x^(-1.72)+42.9`

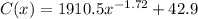
Finding the first derivative.

We can work directly with derivative formulas and we get

`C\, '(x)=1910.5(-1.72)x^(-2.72) \\ C\, '(x)=-3286.06 x^(-2.72)`

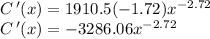
Finding the second derivative.

Applying the derivative one more time we get

`C\, ''(x)=-3286.06(-2.72) x^(-3.72) \\ C\, ''(x)=8938.08 x^(-3.72)`

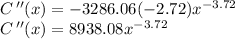
Writing it with positive exponents we get

`C\, ''(x)=\cfrac{8938.08}{ x^(3.72)}`

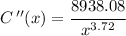
Determining the concavity.

From the interval (5,20), we can pick any value and if we replace it on the second derivative, we will get a positive denominator, and since the numerator is also positive we can conclude that

`C\,''(x) > 0  \text{ for } 5 < x < 20`

Thus since the second derivative is positive on the interval (5, 20), then the graph of C is concave upward on such interval.