Answer:
$9.361 is the smallest amount, approximately.
Explanation:
The given expression is
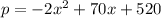
Where
 is profit and
is profit and
 is money.
is money.
Now, with the restriction of making profits of at least $1000, the expression would be
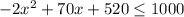
We need to multiply the inequality by -1/2,

Now we solve the quadratic expression
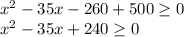
Solving with a calculator, the numbers that satisfy the quadratic expression are approximately
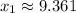 and
and

The image attached shows the graph solution of this inequality.
Therefore, the smallest solution to make a profit of at least $1000 is $9.361.