Question

Many airline companies have begun implementing fees for checked bags. Economic theory predicts that passengers will respond to the increase in the price of a checked bag by substituting carry-on bags for checked bags. As a result, the mean weight of a passenger's carry-on items is expected to increase after the implementation of the checked-bag fee.

Suppose that a particular airline's passengers had a mean weight for their carry-on items of 16 pounds, the FAA standard average weight, before the implementation of the checked-bag fee.

The airline conducts a hypothesis test to determine whether the current mean weight of its passengers' carry-on items is more than 16 pounds. It selects a random sample of 67 passengers and weighs their carry-on items. The sample mean is x = 17.1 pounds, and the sample standard deviation is
s = 6.0pounds. The airline uses a significance level of α =.05 to conduct its hypothesis test.

a. The hypothesis test is _____ test.

- The test statistic follows a _____ distribution. The value of the test statistic is_____.

b. Use the relevant statistical Distributions table to develop the critical value rejection rule.

According to the critical value approach, the rejection rule is:

A. Reject H0 if t ≤ − 1.997 or t ≥ 1.997
B. Reject H0 if z ≥ 1.645
C. Reject H0 if t ≥ 1.668
D. Reject H0 if t ≤ −1.668

c. The p-value is_____.

d. Using the critical value approach, the null hypothesis is _____, because _____ Using the p-value approach, the null hypothesis is_____, because_____ Therefore, you _____ conclude that the mean weight of the airline's passengers' carry-on items has increased after the implementation of the checked-bag fee.

Answer 1

Explanation:

a. The hypothesis test is one tailed_____ test.

(Because we check whether sample weight is greater than hence one tailed or right tailed)

The test statistic follows a __t___ distribution.(Because only sample std deviation s is known)

The value of the test statistic is___Mean difference/Std error =
`(17.1-16)/((6)/(√(67) ) ) \\=1.58`__

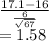b. df = 66

Reject H0 if t ≥ 1.668

c. The p-value is_____0.059444

d. Using the critical value approach, the null hypothesis is _accepted____, because __t <1.668___ Using the p-value approach, the null hypothesis is__accepted___, because__p value <0.05 our significance level.___ Therefore, you __may___ conclude that the mean weight of the airline's passengers' carry-on items has increased after the implementation of the checked-bag fee.