Question

Consider two Carnot heat engines operating in series. The first engine receives heat from the reservoir at 1400 K and rejects the waste heat to another reservoir at temperature T. The second engine receives this energy rejected by the first one, converts some of it to work, and rejects the rest to a reservoir at 300 K. If the thermal efficiencies of both engines are the same, determine the temperature T.

Answer 1

The temperature T= 648.07k

Step-by-step explanation:

T1=input temperature of the first heat engine =1400k

T=output temperature of the first heat engine and input temperature of the second heat engine= unknown

T3=output temperature of the second heat engine=300k

but carnot efficiency of heat engine =
`1 - (Tl)/(Th) \\`

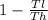
where Th =temperature at which the heat enters the engine

Tl is the temperature of the environment

since both engines have the same thermal capacities
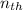`n_(th)` therefore
`n_(th) =n_(th1) =n_(th2)\\n_(th )=1-(T1)/(T)=1-(T)/(T3)\\ \\= 1-(1400)/(T)=1-(T)/(300)\\`

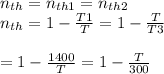
We have now that

`(-1400)/(T)+(T)/(300)=0\\`

multiplying through by T

`-1400 + (T^(2) )/(300)=0\\`

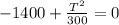
multiplying through by 300

-
`420000+ T^(2) =0\\T^2 =420000\\√(T2)=√(420000)  \\T=648.07k`

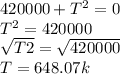
The temperature T= 648.07k