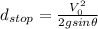Question

A block slides down an inclined plane of slope angle θ with constant velocity. It is then projected up the same plane with an initial speed v0. How far up the incline will it move before coming to rest? (Use any variable or symbol stated above along with the following as necessary: g for the acceleration of gravity.)

Answer 1

The block reaches a distance of
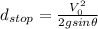`d_(stop) =(V_(0)^2)/(2gsin\theta)` along its upward movement.

Step-by-step explanation:

To set up this question, we need to write down the forces equilibrium equation along the inclined plane. In other words, the key is to project all forces (weight, then gravity vector) onto the inclined plane. Here, we can neglect the previous, downwards movement since initial conditions for the upward movement are given.

The resulting equation is:

`-mgsin(\theta)=ma=m(dv)/(dt)` (all constant values are known, as assumed in question)

Our initial condition is:
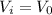`V_(i)=V_(0)` (given data)

Let us integrate this equation:

`\int\limits^t_0 {-mgsin(\theta)} \, dt =\int\limits^t_0 {m(dv)/(dt)} \, dt`

Once initial conditions are applied (for t=0, v=V0),

`-g sin(\theta)t=v-V_(0)`

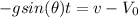
So, assuming no energy dissipaton by friction (between the two solids or other, such as aerodynamic) exists, the time for which speed value reaches zero (block stops) is given for v=0:

`t_(stop)=(V_(0))/(gsin(\theta))`

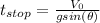
Integrating once again our equation, seeking for a distance equation. we find x (distance) by integrating v (speed), as a function of time:

`d_(stop)=\int\limits^t_0 {v} \, dt =\int\limits^t_0 {(V_(0)-gsin\theta t) \, dt=V_(0)t-gsin\theta t^2/2`

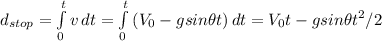
Applying the given time for stop,

`d_(stop) =(V_(0)^2)/(2gsin\theta)`