Answer:
16 cm
Step-by-step explanation:
For protons:
Energy, E = 300 keV
radius of orbit, r1 = 16 cm
the relation for the energy and velocity is given by

So,
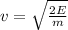 .... (1)
.... (1)
Now,
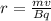
Substitute the value of v from equation (1), we get
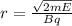
Let the radius of the alpha particle is r2.
For proton
So,
 ... (2)
... (2)
Where, m1 is the mass of proton, q1 is the charge of proton
For alpha particle
So,
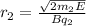 ... (3)
... (3)
Where, m2 is the mass of alpha particle, q2 is the charge of alpha particle
Divide equation (2) by equation (3), we get
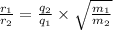
q1 = q
q2 = 2q
m1 = m
m2 = 4m
By substituting the values
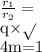
So, r2 = r1 = 16 cm
Thus, the radius of the alpha particle is 16 cm.