Question

A study conducted at a certain college shows that 53% of the school’s graduates find a job in their chosen field within a year after graduation. Find the probability that among 5 randomly selected graduates, at least one finds a job in his or her chosen field within a year of graduating.Take answer from options below:a. 351.96b. 0.1615c. 0.0229d. 0.9582e. 83.85%f. 0.0418g. 97.35%h. 351.08i. 349.05j. 525k. 0.9771l. 81.5%m. 5025.40n. 0.0261o. 238.30p. 68%q. 95%

Answer 1

Answer: 0.977

Explanation:

Given : The proportion of school’s graduates find a job in their chosen field within a year after graduation : p= 0.53

Let x be the binomial variable that represents the number of students finds a job in his or her chosen field within a year of graduating.

with parameter p = 0.53 n= 5

Using binomial , we have

`P(x)=^nC_xp^x(1-p)^(n-x)`

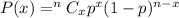
Required probability :-

`P(x\geq1)=1-P(x=0)\\\\=1-^5C_0 (0.53)^0(1-0.53)^5\\\\=1-(0.47)^5\\\\=0.9770654993\approx0.977`

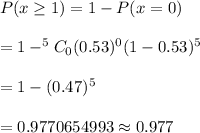
Hence, the probability that among 5 randomly selected graduates, at least one finds a job in his or her chosen field within a year of graduating = 0.977