Answer:
k =

b =
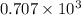
t =
Solution:
As per the question:
Mass of the block, m = 1000 kg
Height, h = 10 m
Equilibrium position, x = 0.2 m
Now,
The velocity when the mass falls from a height of 10 m is given by the third eqn of motion:

where
u = initial velocity = 0
g = 10
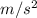
Thus
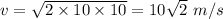
Force on the mass is given by:
F = mg =

Also, we know that the spring force is given by:
F = - kx
Thus
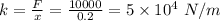
Now, to find the damping constant b, we know that:
F = - bv
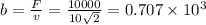
Now,
Time required for the platform to get settled to 1 mm or 0.001 m is given by: