Question

American kestrels live in More Mesa near your professor’s house. Suppose that there are 100 birds, of which a random sample of size 20 your professor has captured and tagged (\simple random sample means that all 100 20 sets of 20 birds are equally likely). The captured birds are returned to the population, and then a new sample is drawn, this time with size 10. This is an important method that is used in ecology, known as capture-recapture. What is the probability that exactly 3 of the 10 birds in the new sample were previously tagged?

Answer 1

P(X=3) = 0.2013

Explanation:

After taking and tagging the first 20 birds, then we have a proportion of 20% of tagged birds within the population, that is

`p=(n)/(N)`

`p=(20)/(100)=0.20`

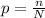
Supposing that the probability (0.20) of capturing a bird remains constant, we may resolve it as it follows:

Capturing 10 birds can be considered as a binomial experiment with a success probability p = 0.2

Let,
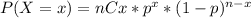`P(X=x)=nCx*p^(x)*(1-p)^(n-x)` be the expression of the binomial distribution, for our case we have:

p=0.2

x = 3

n=10

Then,

`P(X=3)=10C3*0.2^(3)*0.8^(10-3)`

`P(X=x)=0.2013`

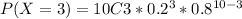
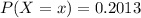
Therefore, the probability that exactly 3 of the 10 birds in the new sample were previously tagged is 20.13%