Question

In this exercise, we estimate the rate at which the total personal income is rising in the Richmond-Petersburg, Virginia, metropolitan area. In 1999, the population in this area was 961400, and the population was increasing at roughly 9200 people per year. The average annual income was 30593 dollars per capita, and this average was increasing at about 1400 dollars per year [a little above the national average of about 1225 dollars yearly] .

Use the Product Rule and these figures to estimate the rate at which the total personal income was rising in the Richmond-Petersburg area in 1999.

Answer: _______________dollars

Answer 1

The rate at which the total personal income was rising in the Richmond-Petersburg area in 1999 is $1.627 billion per year

Explanation:

Let
`t` be the number of years after 1999.

From the information given:

1. In 1999, the population in this area was 961400, and the population was increasing at roughly 9200 people per year.
2. The average annual income was 30593 dollars per capita, and this average was increasing at about 1400 dollars per year.

The population growth can be modeled with a linear equation. The initial population was
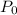`P_0` is 961400 and it grows by 9200 people per year.

The population in time t can be written

`P(t)=9200t+961400`

The average annual income can be modeled with a linear equation. The initial average annual income was 30593 dollars per capita and it grows by 1400 dollars per year.

`A(t)=1400t+30593`

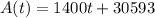
If we multiply both together gives the total personal income at time t.

`T(t)=P(t)\cdot A(t)\\T(t)=(9200t+961400)\cdot (1400t+30593)`

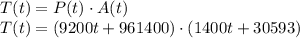
The rate at which the total personal income was rising in the Richmond-Petersburg area is the derivative
`T(t)'`

We need to use the Product Rule that says

If f and g are both differentiable, then:

`(d)/(dx)[f(x)g(x)]=f(x)(d)/(dx)[g(x)] +g(x)(d)/(dx)[f(x)]`

Applying the Product Rule

`(d)/(dt)T(t)=(d)/(dt) [(9200t+961400)\cdot (1400t+30593)]\\\\T(t)'=(d)/(dt)\left(9200t+961400\right)\left(1400t+30593\right)+(d)/(dt)\left(1400t+30593\right)\left(9200t+961400\right)\\\\T(t)'=9200\left(1400t+30593\right)+1400\left(9200t+961400\right)\\\\T(t)'=12880000t+281455600+12880000t+1345960000\\\\T(t)'=25760000t+1627415600`

For 1999, t = 0.

The raising is

`T(0)'=25760000(0)+1627415600\\T(0)'=1,627,415,600`

The rate at which the total personal income was rising in the Richmond-Petersburg area in 1999 is $1.627 billion per year.