Question

A bar 4.0m long weights 400 N. Its center of gravity is 1.5m from on end. A weight of 300N is attached at the light end. What are the magnitude, direction, and point of application of the force needed to achieve transitional and rotatinal equilibruim, of the bar?

Answer 1

The resulting, needed force for equilibrium is a reaction from a support, located at 2.57 meters from the heavy end. It is vertical, possitive (upwards) and 700 N.

Step-by-step explanation:

This is a horizontal bar.

For transitional equilibrium, we just need a force opposed to its weight, thus vertical and possitive (ascendent). Its magnitude is the sum of the two weights, 400+300 = 700 N, since weight, as gravity is vertical and negative.

Now, the tricky part is the point of application, which involves rotational equilibrium. But this is quite simple if we write down an equation for dynamic momentum with respect to the heavy end (not the light end where the additional weight is placed). The condition is that the sum of momenta with respect to this (any) point of the solid bar is zero:

`0=\Sigma_(i)M=400\cdot1.5+300\cdot4-d\cdot700`

Where momenta from weights are possitive and the opposed force creates an oppossed momentum, then a negative term. Solving our unknown d:

`d=(400\cdot1.5+300\cdot4)/(700) =2.57 m`

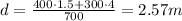
So, the resulting force is a reaction from a support, located at 2.57 meters from the heavy end (the one opposed to the added weight end).