Answer:
0.16
Explanation:
Given that the length of time Y necessary to complete a key operation in the construction of houses has an exponential distribution with mean 18 hours.
The formula for cost of completing this operation is
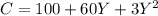
C has mean 3124
Var(C) = 28,460,160
Std dev (C) =
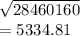
X = 4000 hours
Difference =
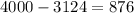
Mean diff/std dev =
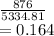
i.e.nearly 0.16 standard deviations above the mean is 4,000 hours