Question

Traffic flow is traditionally modeled as a Poisson distribution.A traffic engineer monitors the traffic flowing through an intersectionwith an average of 6 cars per minute. If 75% of vehiclesare from state, what is the probability that during next 2 minexactly 5 cars passing an intersection are from state?

Answer 1

There is a 6.07% probability that during next 2 min exactly 5 cars passing an intersection are from state.

Explanation:

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

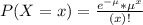
In which

x is the number of sucesses

`e = 2.71828` is the Euler number

`\mu` is the mean in the given time interval.

In this problem, we have that:

A traffic engineer monitors the traffic flowing through an intersection with an average of 6 cars per minute. So in 2 minutes, 12 cars are expected to flow through the intersection.

If 75% of vehiclesare from state, what is the probability that during next 2 min exactly 5 cars passing an intersection are from state?

We want to know how many of these cars are from state. In 2 minutes, 0.75*12 = 9 cars from the state are expected to pass the intersection, so
`\mu = 9`.

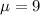We want to find P(X = 2).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 5) = (e^(-9)*9^(5))/((5)!) = 0.0607`

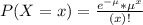
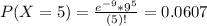
There is a 6.07% probability that during next 2 min exactly 5 cars passing an intersection are from state.