Question

A rigid tank whose volume is 2 m3, initially containing air at 1 bar, 295 K, is connected by a valve to a large vessel holding air at 6 bar, 295 K. The valve is opened only as long as required to fill the tank with air to a pressure of 6 bar and a temperature of 350 K. Assuming the ideal gas model for the air, determine the heat transfer between the tank contents and the surroundings, in kJ

Answer 1

`Q_(cv)=-339.347kJ`

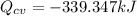
Step-by-step explanation:

First we calculate the mass of the aire inside the rigid tank in the initial and end moments.

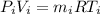`P_iV_i=m_iRT_i` (i could be 1 for initial and 2 for the end)

State1

`1bar*|(100kPa)/(1)|*2=m_1*0.287*295`

`m_1=232kg`

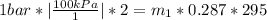
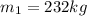
State2

`8bar*|(100kPa)/(1bar)|*2=m_2*0.287*350`

`m_2=11.946`

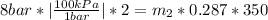
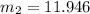
So, the total mass of the aire entered is

`m_v=m_2-m_1\\m_v=11.946-2.362\\m_v=9.584kg`

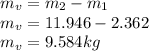
At this point we need to obtain the properties through the tables, so

For Specific Internal energy,

`u_1=210.49kJ/kg`

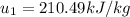
For Specific enthalpy

`h_1=295.17kJ/kg`

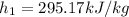
For the second state the Specific internal Energy (6bar, 350K)

`u_2=250.02kJ/kg`

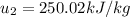
At the end we make a Energy balance, so

`U_(cv)(t)-U_(cv)(t)=Q_(cv)-W{cv}+\sum_i m_ih_i - \sum_e m_eh_e`

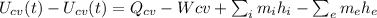
No work done there is here, so clearing the equation for Q

`Q_(cv) = m_2u_2-m_1u_1-h_1(m_v)`

`Q_(cv) = (11.946*250.02)-(2.362*210.49)-(295.17*9.584)`

`Q_(cv)=-339.347kJ`

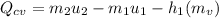
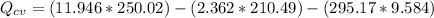
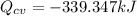
The sign indicates that the tank transferred heat to the surroundings.