Question

37th term; a1 = 2.3; d = -2.3

Answer 1

37th term of given arithmetic sequence
`a_1` = 2.3; d = -2.3 is -80.5.

Solution:

Given that

Need to determine 37th term, when
`a_1` = 2.3, d = -2.3

Means first term of arithmetic sequence =
`a_1` = 2.3 and common difference d = -2.3

Formula for nth term of arithmetic sequence is

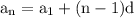`\mathrm{a}_{\mathrm{n}}=\mathrm{a}_(1)+(\mathrm{n}-1) \mathrm{d}` --- equation 1

`\text { In our case } a_(1)=2.3, d=-2.3`

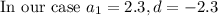
We need to determine 37th term so n = 37.

On substituting given values in equation (1) we get

`\mathrm{a}_(37)=\mathrm{a}_(1)+(37-1) \mathrm{d}`

`\begin{array}{l}{\Rightarrow a_(37)=2.3+(37-1)(-2.3)} \\\\ {\Rightarrow a_(37)=2.3(1-36)=2.3 * 35=-80.5}\end{array}`

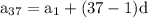
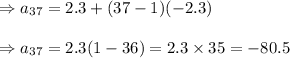
Hence 37th term of given arithmetic sequence is -80.5