Question

The number of entrees purchased in a single order at a Noodles & Company restaurant has had an historical average of 1.35 entrees per order. On a particular Saturday afternoon, a random sample of 26 Noodles orders had a mean number of entrees equal to 1.4 with a standard deviation equal to 0.7. At the 1 percent level of significance, does this sample show that the average number of entrees per order was greater than expected?

a) Calculate the t statistic (Round your answer to 2 decimal places.)
b) Find the p-value. (Round your answer to 4 decimal places.)

Answer 1

a) 0.3571

b) The p-value is 0.362007.

Explanation:

We are given the following in the question:

Population mean, μ = 1.35

Sample mean,
`\bar{x}` = 1.4

Sample size, n = 26

Alpha, α = 0.01

Sample standard deviation, s = 0.7

First, we design the null and the alternate hypothesis

`H_(0): \mu = 1.35\text{ entrees per order}\\H_A: \mu > 1.35\text{ entrees per order}`

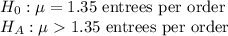
We use One-tailed t test to perform this hypothesis.

a) Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(s)/(√(n-1)) }`

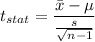
Putting all the values, we have

`t_(stat) = \displaystyle(1.4 - 1.35)/((0.7)/(√(25)) ) = 0.3571`

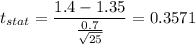
b) The p-value at t-statistic 0.3571 and degree of freedom 25 is 0.362007.