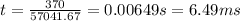Question

A 4.2-g bullet is fired at a speed of 370 m/s into a stationary lead block, which moves a distance of 1.2 m before coming to rest. (a) What is the average force on the bullet after it strikes the block? (b) If this force is constant, how long does it take the bullet to come to rest?

Answer 1

(a) F = 239.575 N (b) t = 0.00649s or 6.49 ms

Step-by-step explanation:

(a) By law of energy conservation, the bullet kinetic energy will be transferred to work done on stopping it from moving.

Formula for Kinetic Energy
`E_k = (mv^2)/(2)` where m is bullet mass, v is the velocity

Formula for work
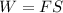`W = FS` where F is the average force and S is the distance travelled.

`E_k = W`

`(mv^2)/(2) = FS`

`F = (mv^2)/(2S)`

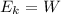
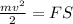
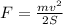
Substitute m = 4.2 g = 0.0042 kg, v = 370 m/s and S = 1.2 (m)

`F = (0.0042*370^2)/(2*1.2) = 239.575 N`

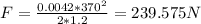
(b) If the force is constant, since the mass is constant and F = ma according to Newton's 2nd law, the acceleration on bullet is also constant

`a = (F)/(m) = (239.575)/(0.0042) = 57041.67 (m/s^2)`

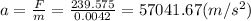
We also have
`v(t) = v_0 + at`

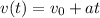
At the time the bullet is coming to rest,
`v(t) = 0, a = -57041.67 m/s^2`

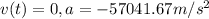
Therefore,
`0 = 370 - 57041.67t`

`t = (370)/(57041.67) = 0.00649 s = 6.49 ms`