Question

A 10 g bullet moving directly upward at 1000 m/s strikes and passes through the center of mass of a 5.00 kg block initially at rest. The bullet emerges from the block moving directly upward at 400 m/s. (a) To what maximum height does the block then rise above its initial position?

(b) What is the average force that the bullet exerts on the block if it takes the bullet 1.40 × 10^−4 s to travel through the block?

Answer 1

0.07339 m

-42857.1428571 N

Step-by-step explanation:

`m_1` = Mass of bullet= 0.01 kg

`m_2` = Mass of block = 5 kg

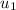`u_1` = Initial Velocity of bullet = 1000 m/s

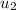`u_2` = Initial Velocity of block = 0 m/s

`v_1` = Initial Velocity of bullet = 1000 m/s

`v_2` = Final Velocity of block

`m_(1)u_(1)+m_(2)u_(2)=m_(1)v_(1)+m_(2)v_(2)\\\Rightarrow v_2=(m_(1)u_(1)+m_(2)u_(2)-m_1v_1)/(m_2)\\\Rightarrow v_2=(0.01* 1000+0-0.01* 400)/(5)\\\Rightarrow v_2=1.2\ m/s`

`KE=PE\\\Rightarrow (1)/(2)mv_2^2=mgh\\\Rightarrow h=(1)/(2)(v^2)/(g)\\\Rightarrow h=(1)/(2)(1.2^2)/(9.81)\\\Rightarrow h=0.07339\ m`

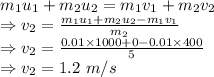
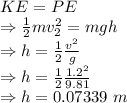
The maximum height the block rises above its initial position is 0.07339 m

`v=u+at\\\Rightarrow a=(v-u)/(t)\\\Rightarrow a=(400-1000)/(1.4* 10^(-4))\\\Rightarrow a=-4285714.28571\ m/s^2`

`F=ma\\\Rightarrow F=0.01* -4285714.28571\\\Rightarrow F=-42857.1428571\ N`

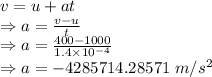
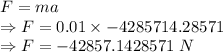
The force that the bullet exerts on the block is -42857.1428571 N