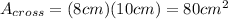Question

If the cylinder has a diameter of 8 cm and a volume of approximately 502.65 cm3, what is the approximate area of the cross-section shown?

A) 40 cm2
B) 60 cm2
C) 80 cm2
D) 100 cm2

Answer 1

It would be 80 because

Answer 2

80 square centimeters.

The volume of a cylinder is defined as:
`V=A.h`

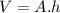
Where
`A` is the area of the base, which is circular:
`A= \pi r^(2)`

If the diameter is
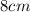`8cm`, then the radius is
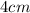`4cm`, because the radius is defines as one half of the diameter. So, area of the base would be:

`A= \pi (4cm)^(2)=16 \pi cm^(2)`

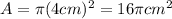
Now, we can calculate the height by replacing all given values in the first equation:

`502.65=16 \pi h\\h=(502.65)/(16 \pi) \\h \approx 10 cm`

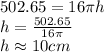
So, we assume that the cross section that's being asked is the rectangular one. The base of the rectangle is the diameter of the as circle 8cm, and the height of the rectangle is the height of the cylinder 10cm.

Therefore, the area of the cross section would be:

`A_(cross)=(8cm)(10cm)=80cm^(2)`