Question

Here is a simple probability model for multiple-choice tests. Suppose that each student has probability p of correctly answering a question chosen at random from a universe of possible questions. (A strong student has a higher p than a weak student.) The correctness of answers to different questions are independent. Jodi is a good student for whom p = 0.85.(a) Use the normal approximation to find the probability that Jodi scores 78% or lower on a 100-question test.(b) If the test contains 250 questions, what is the probability that Jodi will score 78% or lower?

Answer 1

a) The probability that Jodi scores 78% or lower on a 100-question test is 4%.

b) The probability that Jodi scores 78% or lower on a 250-question test is 0.023%.

Explanation:

a) To approximate this distribution we have to calculate the mean and the standard distribution.

The mean is the proportion p=0.85.

The standard deviation can be calculates as:

`\sigma=\sqrt{(p(1-p))/(n) }= \sqrt{(0.85*(1-0.85))/(100) }=0.04`

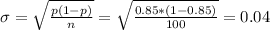
To calculate the probability that Jodi scores 78% or less on a 100-question test, we first calculate the z-value:

`z=(p-p_0)/(\sigma) =(0.78-0.85)/(0.04) =-1.75`

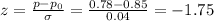
The probability for this value of z is

`P(x<0.78)=P(z<-1.75)=0.04`

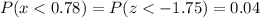
The probability that Jodi scores 78% or lower on a 100-question test is 4%.

b) In this case, the number of questions is 250, so the standard deviation needs to be calculated again:

`\sigma=\sqrt{(p(1-p))/(n) }= \sqrt{(0.85*(1-0.85))/(250) }=0.02`

To calculate the probability that Jodi scores 78% or less on a 250-question test, we first calculate the z-value:

`z=(p-p_0)/(\sigma) =(0.78-0.85)/(0.02) =-3.5`

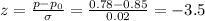
The probability for this value of z is

`P(x<0.78)=P(z<-3.5)=0.00023`

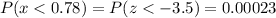
The probability that Jodi scores 78% or lower on a 250-question test is 0.023%.