Answer:
T=655K, W=816kJ/kg
Step-by-step explanation:
consulting the properties of gases, for Helium we have,
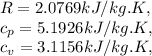
To find the specific volume we use the equation,
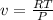
Substituting,
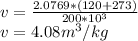
Flow work is gived by,
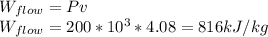
To find the temperature of the gas in the tank we need
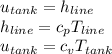
So,
