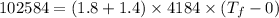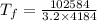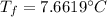Answer:
Step-by-step explanation:
Given:
- mass of the tea,
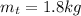
- temperature of the tea,
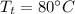
- mass of ice,
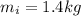
- temperature of the ice,
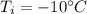
We, know
- specific heat of tea(water),
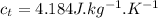
- specific heat of ice,

- Latent heat of fusion of ice,
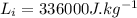
Heat required for warming of ice upto 0°C from -10°C
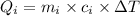
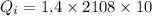
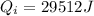
Heat released during the cooling of tea upto 0°C from 80°C
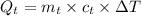
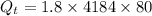
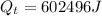
∵
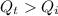
∴The heat from the quantity that remains after bringing the ice to 0°C will be used for melting the ice.
Heat remaining afterthis process:
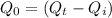 = 572984 J
= 572984 J
Amount of heat energy required by the total mass of ice to melt at 0°C:
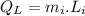

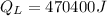
Now, the remaining of the heat will be used to raise the temperature of the tea (water) from 0°C to a higher temperature.
Heat remaining after melting the total ice into water at 0°C which will increases the temperature of water:
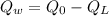
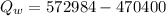
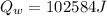
Now, the final temperature of the tea(water)rising from 0°C:
∵whole ice(along with tea) is now water with initial temperature
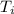 = 0°C
= 0°C
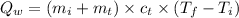
where:
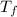 = final temperature
= final temperature