Question

Gibbons, small Asian apes, move by brachiation, swinging below a handhold to move forward to the next handhold. A 8.7 kg gibbon has an arm length (hand to shoulder) of 0.60 m. We can model its motion as that of a point mass swinging at the end of a 0.60-m-long, massless rod. At the lowest point of its swing, the gibbon is moving at 3.7 m/s. What upward force must a branch provide to support the swinging gibbon?

Answer 1

198.505 N

Step-by-step explanation:

Since this can be modeled as a point mass swinging system with the radius being the arm length. So r = 0.6m.

Also at it's lowest point the ape has a horizontal velocity v = 3.7 m/s. This velocity could result in a centripetal acceleration a, creating tension on the branch.

`a = (v^2)/(r)`

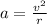
According to Newton's 2nd law, F = ma. So the tension is:

`F = ma = (mv^2)/(r) = (8.7*3.7^2)/(0.6) = 198.5N`