Question

Suppose the U.S. president wants an estimate of the proportion of the population who support his current policy toward revisions in the health care system. The president wants the estimate to be within 0.03 of the true proportion. Assume a 90% level of confidence. The president's political advisors estimated the proportion supporting the current policy to be 0.06.

a.
How large of a sample is required? (Round up your answer to the next whole number.)

Answer 1

Answer: 170

Explanation:

As per given , we have

The prior estimate to true population proportion:
`p=0.06`

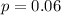
Critical value for 90% confidence =
`z_(\alpha/2)=1.645`

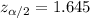
[using z-value table.]

Margin of error : E= 0.03

Formula to find the required sample size : -

`n=p(1-p)((z_(\alpha/2))/(E))^2\\\\=0.06(1-0.06)((1.645)/(0.03))^2\\\\=169.577566667\approx170`

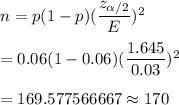
Hence, the required minimum sample = 170