Question

There are four​ suits: clubs,​ diamonds, hearts, and​ spades, and the following cards appear in each​ suit: Ace,​ 2, 3,​ 4, 5,​ 6, 7,​ 8, 9,​ 10, Jack,​ Queen, King. The​ Jack, Queen, and King are called face cards because they have a drawing of a face on them. Diamonds and hearts are​ red, and clubs and spades are black. If you draw 1 card randomly from a standard​ 52-card playing​ deck, what is the probability that it will​ be:

a. A 4
b. A black card
c. A diamond
d. A none- face card

Answer 1

a. 4/52

b. 1/2

c. 1/4

d. 10/13

Explanation:

In order to obtain the probabilities, you have to apply the formula:

`P(A) = (n(A))/(n)`

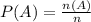
Where P(A) is the probability of an event A, n(A) is the number of favorable outcomes for the event and n is the total number of possible outcomes.

For part a:

The total number of 4 cards is 4, because there are four suits and a card 4 for each suit

n(a)= 4

n=52 (The total number of cards)

P(a)=4/52

For part b:

There are two suits with black cards and 13 cards in each suit. Therefore, the number of black cards is: 13(2)=26

n(b)=26

n=52

P(b)=26/52=1/2

For part c:

The total number of cards with diamonds is 13

n(c)=13

n=52

P(c)=13/52=1/4

For part d:

There are 3 face cards in each suit, therefore the total number of face cards is (3)(4)=12. The rest of the cards are none-face cards, therefore:

n(d)= 52-12 = 40

n=52

P(d)=40/52=10/13