Answer:
D(11) = 37.660 m
dD/dt = 2.7260 m/s
Step-by-step explanation:
given data
two path apart = 17 m
walks east one path = 4 km/h = 1.111 m/s
walks west other path = 7 km/h = 1.944 m/s
pass each other time t = 0
solution
we consider here east is the positive direction and west is the negative direction
so that
the east - west distance between them is = 1.111 + 1.944 = 3.055 m/s
and
the actual distance between them time t is
D(t) =
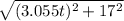
at time 11 s
D(11) =
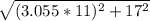
D(11) = 37.660 m
and
increase rate is dD/dt
dD/dt =
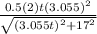
so for 11 sec
dD/dt =
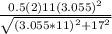
dD/dt = 2.7260 m/s