Answer:
The true velocity of wind will be 43.1 km/h.
Step-by-step explanation:
Given that,
Velocity of motor
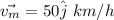
The resultant velocity of wind
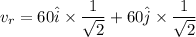
Suppose, the true velocity of wind is
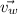 .
.
We need to calculate the true velocity of wind
Using formula of resultant velocity
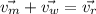
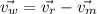
Where,
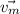 = velocity of motor
= velocity of motor
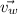 = velocity of wind
= velocity of wind
 = resultant velocity
= resultant velocity
Put the value into the formula
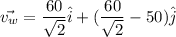
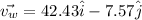
The magnitude of true velocity is,
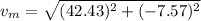
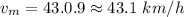
Hence, The true velocity of wind will be 43.1 km/h.