Final Answers:
1) The mass will be moving at the bottom of its path at a speed of v = 6.82 m/s.
2) The magnitude of the tension in the string at the bottom of the path is T = 90.8 N.
3) If the maximum tension the string can take is Tmax = 382 N, the maximum mass that can be used is m_max = 24.95 kg.
4) The mass will be moving at the top of its new path above the peg at a speed of v = 5.32 m/s.
Step-by-step explanation:
1) To find the speed of the mass at the bottom of its path, we can use the principle of conservation of energy. At the bottom, all the potential energy is converted into kinetic energy. The potential energy at the top (when the pendulum is horizontal) equals the kinetic energy at the bottom. So,
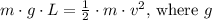 is the acceleration due to gravity and
is the acceleration due to gravity and
 is the length of the rope. Solving for
is the length of the rope. Solving for
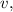 we get
we get
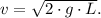
2) The tension in the string at the bottom of the path is maximum when the pendulum is at its lowest point. At this point, the tension is the sum of the weight of the mass and the centripetal force required to keep it moving in a circular path. Thus,
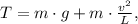 where
where
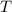 is tension,
is tension,
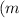 is mass,
is mass,
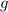 is gravity,
is gravity,
 is speed, and
is speed, and
 is the length of the rope.
is the length of the rope.
3) Using the equation for tension
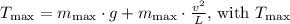 given, rearrange the equation to solve for
given, rearrange the equation to solve for
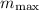 . Plug in the known values to find the maximum mass that can be used.
. Plug in the known values to find the maximum mass that can be used.
4) To find the speed of the mass at the top of its new path, we need to use the conservation of mechanical energy. The total mechanical energy at the bottom of the swing (kinetic energy + potential energy) will be equal to the total mechanical energy at the top of the new path. Use the appropriate forms of energy at each point to calculate the speed at the top of the new path.