Question

A circular saw blade with radius 0.175 m starts from rest and turns in a vertical plane with a constant angular acceleration of 2.00 rev/s^2. After the blade has turned through 155 rev, a small piece of the blade breaks loose from the top of the blade. After the piece breaks loose, it travels with a velocity that is initially horizontal and equal to the tangential velocity of the rim of the blade. The piece travels a vertical distance of 0.820 m to the floor.

(A) How far does the piece travel horizontally, from where it broke off the blade until it strikes the floor? Express your answer with the appropriate units.

L = ?

Answer 1

The distance the piece travel in horizontally axis is

L=3.55m

Step-by-step explanation:

`a=2 (rev)/(s^(2)) \\h=0.820m\\r = 0.125 m \\d=150rev`

`d= 155 rev = 155(2\pi ) = 310\pi rad`

`a= 2.0 (rev)/(s^(2) ) = 2.0(2\pi )  = 4.0\pi (rev)/(s^(2) )`

`d=d_(i)+vo*t+(1)/(2)*a*t^(2) \\ di=0\\vo=0\\d=(1)/(2)*a*t^(2)\\t=\sqrt{(2*d)/(a)}\\t=\sqrt{(2*310 rad)/(4(rad)/(s^(2)))} \\t=12.449`

`w=a*t\\w=4(rad)/(s^(2))*12.449s\\ w=49.79 (rad)/(s)`

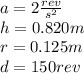
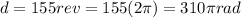
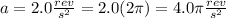
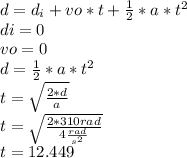
Now the angular velocity is the blade speed so:

`V=w*r\\V=49.79 (rad)/(s)*0.175m\\V=8.7 (m)/(s)`

assuming no air friction effects affect blade piece:

time for blade piece to fall to floor

`t=\sqrt{(2*h)/(g)}\\t=\sqrt{(2*0.820m)/(9.8(m)/(s^(2) ) )}\\t=0.409s`

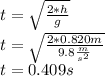
Now is the same time the piece travel horizontally

`L=t*V\\L=0.409s*8.7(m)/(s)\\L=3.55m`

blade piece travels HORIZONTALLY = (24.5)(0.397) = 9.73 m ANS