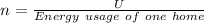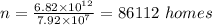Question

Compressed air can be pumped underground into huge caverns as a form of energy storage. The volume of a cavern is 4.40 105 m3, and the pressure of the air in it is 6.20 106 Pa. Assume that air is a diatomic ideal gas whose internal energy U is given by U = 5/2 nRT. If one home uses 22.0 kW · h of energy per day, how many homes could this internal energy serve for one day?

Answer 1

86112 homes

Solution:

As per the question:

Volume, V =
`4.40* 10^(5)\ m^(3)`

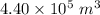
Pressure, P =
`6.20* 10^(6)\ Pa`

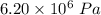
Internal energy, U =
`(5)/(2)nRT`

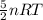
Energy usage of one home = 22.0 kWh

Now,

We know from the ideal gas equation:

PV = nRT

Thus we can write:

`U = (5)/(2)nRT = (5)/(2)PV`

`U = (5)/(2)PV = (5)/(2)* 6.20* 10^(6)* 4.40* 10^(5) = 6.82* 10^(12) J`

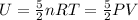
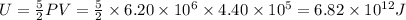
Energy usage of one home =
`22* 1000* 3600 = 7.92* 10^(7) J`

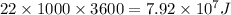
Now,

No. of homes that could serve this internal energy for a day is given by:

`n = (U)/(Energy\ usage\ of\ one\ home)`

`n = (6.82* 10^(12))/(7.92* 10^(7)) = 86112\ homes`