Question

Students conducted an experiment to determine whether the Belgium-minted Euro coin was equally likely to land heads up or tails up. Coins were spun on a smooth surface, and in 290 spins, 160 landed with the heads side up. Should the students interpret this result as convincing evidence that the proportion of the time the coin would land heads up is not 0.5? Test the relevant hypotheses using α = 0.01. Would your conclusion be different if a significance level of 0.05 had been used? (Round your test statistic to two decimal places and your P-value to four decimal places.)

Answer 1

Explanation:

No of trials = 290

no of heads =160

Sample proportion p =
`(160)/(290) =0.552`

`H_0: p=0.5\\H_a: p \\eq 0.5`

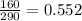
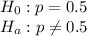
(Two tailed test)

p difference =
`0.552-0.5=0.052`

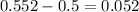
Std error =
`\sqrt{(0.5(0.5))/(290) } \\=0.02936`

Z statistic = 1.77

p value = 0.076

p value >0.05 hence accept that prob for heads is 0.5

If it is 1%p>0.01 hence accept null hypothesis again