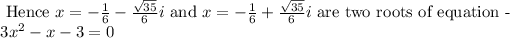Question

Use the quadratic formula to solve the following equation -3x^2-x-3=0

Answer 1

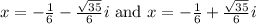`x=-(1)/(6)-(√(35))/(6) i \text { and } x=-(1)/(6)+(√(35))/(6) i` are two roots of equation
`-3 x^(2)-x-3=0`

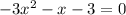
Solution:

Need to solve given equation using quadratic formula.

`-3 x^(2)-x-3=0`

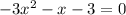
General form of quadratic equation is
`a x^(2)+b x+c=0`

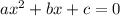
And quadratic formula for getting roots of quadratic equation is

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

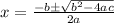
In our case b = -1 , a = -3 and c = -3

Calculating roots of the equation we get

`\begin{array}{l}{x=\frac{-(-1) \pm \sqrt{(-1)^(2)-4(-3)(-3)}}{2 *-3}} \\\\ {x=-(1)/(6) \pm\left(-(√(-35))/(6)\right)}\end{array}`

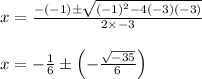
Since
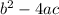`b^(2)-4 a c` is equal to -35, which is less than zero, so given equation will not have real roots and have complex roots.

`\begin{array}{l}{\text { Hence } x=-(1)/(6)-(√(35))/(6) i \text { and } x=-(1)/(6)+(√(35))/(6) i \text { are two roots of equation - }} \\ {3 x^(2)-x-3=0}\end{array}`