Question

A manufacturer of small appliances purchases plastic handles for coffeepots from an outside vendor. If a handle is cracked, it is considered defective and must be discarded. A large shipment of plastic handles is received. The proportion of defective handles p is of interest. How many handles from the shipment should be inspected to estimate p to within 0.09 with 95% confidence?

Answer 1

Answer: 119

Explanation:

Since the prior estimate of population proportion of defective handles (p) is unknown , so we take p= 0.5

Given : Margin of error : E=0.09

Critical value for 95% confidence interval :
`z_(\alpha/2)=1.96`

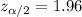
Required sample size :-

`n=0.5(1-0.5)((z_(\alpha/2))/(E))^2\\\\=0.25((1.96)/(0.09))^2\\\\=118.567901235\approx119`

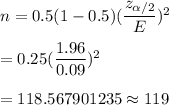
Hence, the minimum sample size required = 119

i.e. 119 handles from the shipment should be inspected.