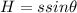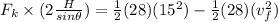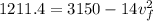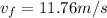Answer:
Part a)
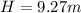
Part B)
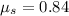
since the required static coefficient is more then the given value so it will not remain at rest at highest position.
Part c)
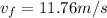
Step-by-step explanation:
Frictional force on the rock while it is moving upwards along the plane is given as
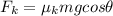
now we have
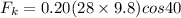
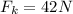
now by energy conservation we can say
Work done by friction = loss in mechanical energy
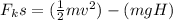
here we know that
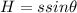
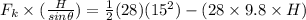

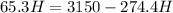
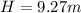
Part B)
Now at the maximum height position we can say that force due to static friction must be balanced by its weight along the plane
so we will have
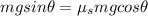
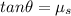
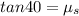
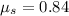
since the required static coefficient is more then the given value so it will not remain at rest at highest position.
Part c)
Again by mechanical energy conservation law
Work done by friction = loss in mechanical energy
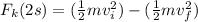
here we know that