Question

A circuit consists of a series combination of 6.00-kΩ and5.00-kΩ resistors connected across a 50.0-V battery havingnegligible internal resistance. You want to measure the truepotential difference (that is, the potential difference without themeter present) across the 5.00-kΩ resistor using a voltmeterhaving an internal resistance of 10.00 kΩ. (a) What potentialdifference does the voltmeter measure across the 5.00-kΩresistor? (b) What is the true potential difference across thisresistor when the meter is not present? (c) By what percentage isthe voltmeter reading in error from the true potentialdifference?

Answer 1

(a) 17.87 V

(b) 22.73 V

(c) 21.38%

Solution:

As per the question:

Voltage of the battery, V = 50.0 V

Now, across the resistance of 5.00
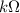`k\Omega`, a battery is connected in parallel with an internal resistance 10.00
`k\Omega`

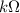
Thus the equivalent resistance of this parallel combination is given by:

`(1)/(R_(eq)) = (1)/(5) + (1)/(10)`

`R_(eq) = (5* 10)/(5 + 10) = 3.34\ k\Omega`

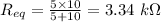
the overall equivalent resistance across 50.0 V is:

`R_(eq) = 3.34 + 6.00 = 9.34\ k\Omega`

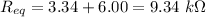
Now, the Current flowing in the circuit is given by:

`I = (V)/(R_(eq)) = (50.0)/(9.34* 10^(3)) = 5.35* 10^(- 3)\ A = 5.35\ mA`

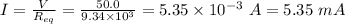
(a) To calculate the potential difference across
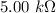`5.00\ k\Omega`, we use Ohm' law:

V = IR =
`5.35* 10^(- 3)* 3.34* 10^(3) = 17.87\ V`

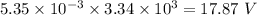
(b) To calculate the true potential difference in absence of the meter across the resistor:

When the meter is not connected, then both the resistors are in series and hence the resultant resistance is :

R' = 6.00 + 5.00 = 11.00
`k\Omega`

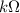
Now, the current in the circuit:

`I' = (V)/(R') = (50)/(11* 10^(3)) = 4.55* 10^(- 3)\ A = 4.55\ mA`

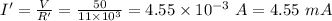
Now, the true potential difference is:

V' = I'R =
`4.55* 10^(- 3)* 5* 10^(3) = 22.73\ V`

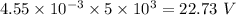
(c) Error in the reading of the voltmeter is given by:

`error = (V' - V)/(V') = (22.73 - 17.87)/(22.73) = 0.2138`

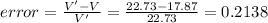
% error = 21.38 %