Question

Two rods are made of brass and have the same length. The cross section of one of the rods is circular, with a diameter 2a. The other rod has a square cross section, where each side of the square is a length 2a. One end of the rods is attached to an immovable fixture which allows the rods to hang vertically. To the free end of each rod, a block of mass m is attached. Which rod, if either, will stretch more after the block is attached?

Answer 1

Answer:Circular cross-section

Step-by-step explanation:

Given

Two rods of brass having circular and square cross-section

Diameter of circular cross-section=2 a

Cross-section
`A_c=(\pi (2a)^2)/(4)=\pi a^2`

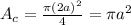
length of square=2 a

Cross-section
`A_s=(2a)^2=4a^2`

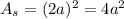
Change in Length of rod
`=(PL)/(AE)`

`\delta L\propto (1)/(A)`

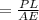
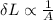
considering all other factors remaining same

Area of cross-section of circular rod is less than the area of cross-section of square rod

thus elongation is more in circular rod