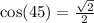Question

Does anyone know how to solve this?

Answer 1

`(√(2))/(2)`

Explanation:

This almost looks like the left hand side of the following identity:

`\sin(A)\cos(B)-\sin(B)\cos(A)=\sin(A-B)` .

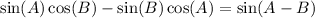Here are similar identities in the same category as the above:

`\sin(A)\cos(B)+\sin(B)\cos(A)=\sin(A+B)`

`\cos(A)\cos(B)-\sin(A)\sin(B)=\cos(A+B)`

`\cos(A)\cos(B)+\sin(A)\sin(B)=\cos(A-B)`

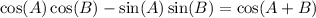
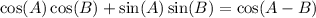
Things to notice: 90-76=14. and 90-59=31.

This means we will possibly want to use the following co-function identities:

`\cos(90-A)=\sin(A)`

`\sin(90-A)=\cos(A)`

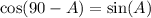
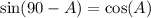
So let's begin:

`\sin(76)\cos(31)-\sin(14)\cos(59)`

Applying the co-function identities:

`\cos(14)\cos(31)-\sin(14)\sin(31)`

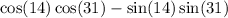
Applying one of the difference identities above with cosine:

`\cos(31+14)`

`\cos(45)`

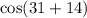
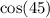
45 is a special angle so
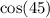`\cos(45)` is something you find off most unit circles in any trigonometry class.

`\cos(45)=(√(2))/(2)`