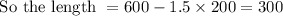Question

A rectangular field is to be enclosed by a fence and divided into two smaller fields by a fence parallel to one side . If 1200m of fence are avaliable, find the dimensions of the field giving the maximus area.

Answer 1

Maximum dimensions of the field be 300m of length and width be 200 maximum area is
`60000 m^(2)`.

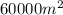Explanation:

2L + 3W = 1200

2L = 1200-3W

Dividing both sides by 2

`\mathrm{L}=(600-1.5 \mathrm{W}) \text { we know area of a rectangle is Length } * \text { Width }`

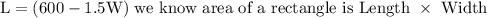
Replace L with (600-1.5W) A = W (600-1.5W) A =
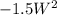`-1.5 W^(2)` + 600W Axis of symmetry,
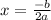`x=(-b)/(2 a)` in this equation: a=-1.5, b=600 we get W = 200.

`\text { So the length }=600-1.5 * 200=300`

`\text { Therefore the maximum area of the field is }-1.5 * 200^(2)+600 * 200=60,000 \mathrm{m}^(2)`