Answer:
1034.78 m
Step-by-step explanation:
The shortest distance is the displacement of the car from initial position to final position.
Displacement of body is given using Newton's equations of motion.
Given:
Initial velocity,
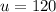 m/s
m/s
Final velocity,
 m/s( As the car stops in its final position)
m/s( As the car stops in its final position)
Coefficient of static friction,

Acceleration due to gravity,
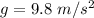
Now, when brakes are applied, only friction acts on the body in a direction opposite to that of its motion.
The acceleration of the car when friction acts the stopping force is given as:
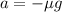 .
.
The acceleration is negative as it reduces the velocity of the motion and acts in the direction opposite to that of the motion.
Plug in 0.71 for
 and 9.8 m/s² for
and 9.8 m/s² for
 . Solve for
. Solve for
 .
.
So,
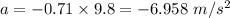 .
.
Now, displacement of the car is given using the following equation of motion:
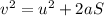
Here,
 is the displacement of the racing car.
is the displacement of the racing car.
Plug in 120 m/s for
 , 0 m/s for
, 0 m/s for
 , -6.958 m/s² for
, -6.958 m/s² for
 . Solve for
. Solve for
 . This gives,
. This gives,
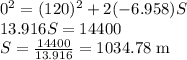
Therefore, the shortest distance in which she can brake and stop is 1034.78 m.