Question

2017 poll found that 56​% of college students were very confident that their major will lead to a good job. If 20 college students are chosen at​ random, what's the probability that 13 of them were very confident their major would lead to a good​ job? Let a success be a college student being very confident their major would lead to a good job.

Answer 1

Answer: 0.1318

Explanation:

Given : The proportion of college students were very confident that their major will lead to a good job : p= 0.56

Let x be the binomial variable (for success) that represents the number of college students were very confident that their major will lead to a good job.

with parameter p = 0.56 n= 20

Using binomial , we have

`P(x)=^nC_xp^x(1-p)^(n-x)`

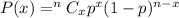
Required probability :-

`P(x=13)=^(20)C_(13)(0.56)^(13)(1-0.56)^(20-13)\\\\=(20!)/(13!7!)(0.56)^(13)(0.44)^(7)\\\\=0.131833824312\approx0.1318`

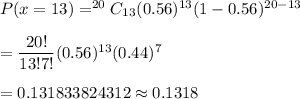
Hence, the probability that 13 of them were very confident their major would lead to a good​ job =0.1318