Question

A university with a high water bill is interested in estimating the mean amount of time that students spend in the shower each day. In a sample of 12 students, the average time was 5.04 minutes and the standard deviation was 0.96 minutes. Using this sample information, construct a 99% confidence interval for the mean amount of time that students spend in the shower each day. Assume normality. a) What is the lower limit of the 99% interval? Give your answer to three decimal places. b) What is the upper limit of the 99% interval? Give your answer to three decimal places.

Answer 1

Answer with explanation:

As per given , we have

`\overline{x}=5.04`

`s=0.96`

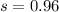
n=12

df = 12-1=11

Since population standard deviation is unknown , so we use t-test.

Critical t-value for 99% confidence (1% significance):

`t_(\alpha/2, df)=t_(0.005,12)=3.1058`

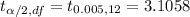
Confidence interval for population mean :_

`\overline{x}\pm t_(\alpha/2)(s)/(√(n))\\\\=5.04\pm (3.1058)(0.96)/(√(12))\\\\\approx5.04\pm0.861\\\\= (5.04-0.861,\ 5.04+0.861)\\\\=(4.179,\ 5.901)`

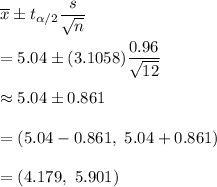
Hence, the 99% confidence interval for the mean amount of time that students spend in the shower each day. Assume normality.=
`(4.179,\ 5.901)`

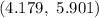
a) Lower limit of the 99% interval = 4.179

b) Upper limit of the 99% interval = 5.901