Question

What is an equation of the line that passes through the point (−1,4) and is parallel to the line 2x+y=1?

Answer 1

y=-2x+2 (if you need it in y-intercept form)

2x+y=2 (if you need it in standard form)

Explanation:

1. Write the original line in y=mx+b form. In other words, get the y by itself on the left side of the equation.

Subtract 2x from both sides.

y=-2x+1

2. Recall that parallel lines have the same slope. Slope is always the number with the x in the equation. Since the slope in the first equation is -2, the slope of the new line will also be -2.

3. Find the y-intercept. Use the point (-1,4) and plug the y and x values into the point-slope formula. M represents the slope.

y-y1=m(x-x1)

y-4=-2(x+1)

Simplify the equation.

y-4=-2x-2

y=-2x+2

(Proceed to step 4 if you need it in standard form)

4. Write the equation in standard form (x+y=z). Z represents the number by itself without variables.

Add -2x to both sides

2x+y=2

Answer 2

An of line that passes through the point (−1,4) and is parallel to the line will be:

• 
  `y=-2x+2`

Explanation:

We know that the slope-intercept form of the line equation

y = mx+b

where m is the slope and b is the y-intercept

Given the line

2x+y=1

converting the line into slope-intercept form

y = -2x+1

comparing with the slope-intercept form of the line equation

The slope of the line = m = -2

We know that the parallel lines have the same slopes.

Thus, the slope of line that passes through the point (−1,4) and is parallel to the line will be: -2

using the point-slope form of the line equation

`y-y_1=m\left(x-x_1\right)`

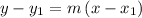
where m is the slope of the line and (x₁, y₁) is the point

substituting the values of the slope = -2 and the point (-1, 4)

`y-y_1=m\left(x-x_1\right)`

`y-4=-2\left(x-\left(-1\right)\right)`

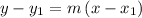
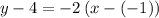
Add 4 to both sides

`y-4+4=-2\left(x+1\right)+4`

`y=-2x+2`

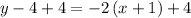
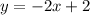
Therefore, an of line that passes through the point (−1,4) and is parallel to the line will be:

• 
  `y=-2x+2`